Another week another programming language (yay!). This week it was Kotlin, a very clean and concise language that is fully interoperable with Java, and the language that Professor Bowers has been developing his circle packing code library in. We’ve been working with IntelliJ IDEA, a Java IDE that understands many other languages as well, including Kotlin, and also contains a nice automated Java-to-Kotlin converter built right into the IDE. Having done some work in Processing over the past two weeks, this has made transferring some fragments of code over to IntelliJ and into Kotlin much easier, especially as I got more acquainted with the language.
One cool thing that I worked on this week was integrating my convex hull code from last week into Professor Bowers’ circle packing code library, so that we could compute the convex hull of points known as the “conical caps” on a sphere. Last week, I had created a Java program in Processing that computed the convex hull of points located three dimensional space. So, this week I worked on transferring my code over to the Kotlin library, which involved changing quite a few things to make sure that it worked correctly. Once integrated, I was able to run an example where I chose four disks on the sphere, obtained their corresponding dual “conical cap” points, and then use my convex hull code to compute the hull of these four points. Here’s a picture to hopefully make some sense out of that.

Once I finished the convex hull section, I then worked on creating a class for three dimensional circular arcs to include in the library. While we already had a class for circular disks (circles) on the sphere, we did not have a class that would store only an arc from a source point to a target point. The implementation of the class itself was very straightforward, as it drew upon the properties of the disk class that had already been implemented. The more difficult part was adding a function to draw a circular arc, given the two points — the source and target — and the disk that the arc was a part of. This involved using Processing’s arc() function — however, this function only draws arcs in two dimensions. To draw three dimensional circular arcs, we therefore had to translate the drawing frame the appropriate way depending on the orientation of the arc, as well as compute the angles from the x-axis to the source and target points of the arc, which required a little bit of linear algebra and trig due to the three dimensional coordinates.
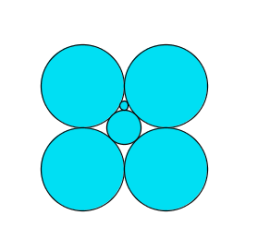
Last major task for the week was creating a program that would actually compute a circle packing. For this, I went back to Processing, and first fixed up a basic graph class that I had started last week. Then I worked on a basic circle packing program, which, given a graph specifying a set of vertices (each associated with a circle), edges (tangency relationships between the circles), and desired radii of boundary circles, would compute the unique radii of the interior circles necessary for the packing to be a valid one. I then tested an easy-to-check example of a packing with four boundary circles with radius of 0.5, and two interior circles, one in the center, tangent to all four boundary circles, and a smaller circle in one of the interstices formed by the interior circle and two boundary circles. Here is a picture of the basic packing example (scaled up a bit).
With the 3D circular arc class now in place, and with some of the other headway this week, hopefully we will be able to get a Voronoi diagram coded and running relatively soon. Can’t wait to see what next week has in store!

Sounds great Sarah – good work. I am impressed with how much code it appears you have already written that works! I will be in on Monday meeting with Dr. Rahman and Dr. Simmons. Hope to catch you in person then. Dr. Weikle
LikeLike